▶︎

all

running...

Last Updated On: 2020-07-11 16:21

Bayes Theorem : A Deep dive Guide

$P(A|B) = \frac{P(B|A)P(A)}{P(B)} \tag{1}$

If hypothesis A is a Random event space from a bigger sample space $A = \{A_1, A_2, ..., A_n\}$ .

$P(A_i|B) = \frac{P(B|A_i)P(A_i)}{P(B)} \hspace{30pt} \forall \hspace{30pt} A = \{A_1, A_2, ..., A_n\} \tag{2}$

$p(a|b) = \frac{p(b|a)P(a)}{p(b)} \tag{3}$

Total Probility in different cases
$P(B) = P(B|A)P(A) + P(B|\neg A)P(\neg A)$
$P(B) = \sum_{j}^{N} P(B|A_j)P(A_j)$
$p(B) = \int\int...\int_{a} P(b|a)P(a) \hspace{30pt} \forall \hspace{30pt} a = \{a_1,a_2,a_3,...,a_n\}$

Equation	Name	Meaning
$P(A \vert B)$	posterior probabilty	Probability of the hypothesis A, given some evidence B
$P(B \vert A)$	likelihood	Probability of the evidence if hypothesis is true
$P(A)$	prior probability	Probability that hypothesis is true without any constraints (also called as initial probability)
$P(B)$	total probality	Probability of the evidence B

Its Derivation

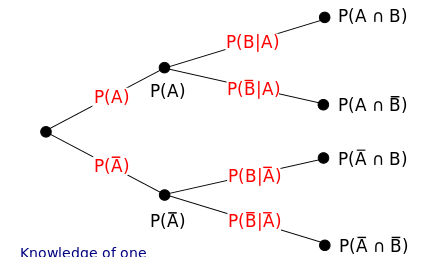
bayes_tree

$\begin{aligned} P(A \cap B) &= P(B \cap A) \\ P(A|B)P(B) &= P(B|A)P(A) \\ P(A|B) &= \frac{P(B|A)P(A)}{P(B)} \end{aligned}$

Equation	Name
$P(A\vert B)$	Conditional Probabilty
$P(A \cap B)$	Joint Probability